Quantitätsgleichung der Geldpolitik von Prof. Urs Birchler erklärt
Prof. Dr. Urs Birchler erklärt die wichtige Quantitätsgleichung der Geldpolitik in einfachen Grafiken. Die Quanitätsgleichung ist eine wichtige Hilfe, um die Geldpolitik zu verstehen, vom Mittelalter bis in unserer Zeit.

Wie viel Geld braucht die Wirtschaft?
Zunächst eine Geschichte:
Anna verkauft mit ihrer Mutter auf dem Markt Äpfel. Am Abend rechnet sie ab: Fünfzig Kilo, verkauft zu je 6 Franken. Gibt 300 Franken. Soviel liegt in der Kasse. Der Umsatz ist also gleich Menge, genannt Q (für Quantität), mal Preis, genannt P.
Anna hat sich auch ein bisschen gelangweilt. Insgeheim hat sie die eingenommenen Banknoten unterschrieben. Als sie eine Woche später wieder am Marktstand hilft, staunt sie: Ein Kunde zahlt mit einer Note, auf der Annas Unterschrift steht. Die Note ist also in der Zwischenzeit in der Wirtschaft zirkuliert und zufällig wieder bei ihr gelandet.
Anna denkt nach: Einen Apfel kann man nur einmal essen, aber eine Banknote kann man offensichtlich zweimal brauchen. Oder dreimal oder immer wieder. Je öfter eine Note pro Jahr die Hand wechselt, desto weniger Geld braucht es.
Sie zieht ihren Stift aus der Tasche und notierte: Menge (Q) mal Preis (P) ist gleich vorhandene Geldmenge (M für money) mal wie oft das Geld ausgegeben wird (V für Velocity, Geschwindigkeit). Beide Seiten der Gleichung messen den Umsatz, einmal von der Güterseite her, einmal von der Geldseite her.
Diese Gleichung heisst Quantitätsgleichung. Chinesische Denker formulierten sie schon vor zweieinhalbtausend Jahren. Geldmangel und Geldüberfluss in der Wirtschaft beschäftigen die Menschen schon seit jeher. Die Gleichung ist auch einfach zu verstehen. Sie funktioniert nämlich wie eine Waage.
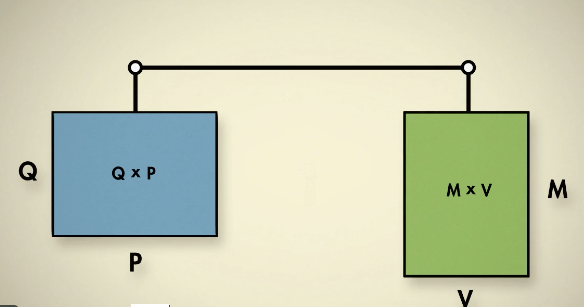
Quantität mal Preis gleich Geldmenge mal Geschwindigkeit
Beginnen wir im Mittelalter. Im Mittelalter herrscht in Europa ein Mangel an Münzmetall. Die Metall-Minen gaben wenig her. Zudem fliessen Edelmetalle ins Morgenland als Preis für Gewürze und andere Luxusgüter. Die Münzen schlägt man deshalb aus billigen Metallen, ganz dünn und oft nur einseitig. Trotzdem geht die Geldmenge zurück (-M). Die Händler müssen ihre Preise senken (-P) oder weniger verkaufen (-Q). Der Geldmangel ist deshalb vielleicht die Ursache des «dunklen Mittelalters».
Doch bald gibt es zum Geldmangel ein Gegengift: Bankiers wie die Medici in Florenz erfinden die bargeldlose Zahlung, zum Beispiel mittels Handelswechsel. Solche Zahlungsversprechen lassen das Geld virtuell zirkulieren; dessen Umlaufsgeschwindigkeit steigt (+V). Die Händler können mehr verkaufen oder höhere Preise verlangen. Die Wirtschaft blüht (+Q).
Bald ist die Geldknappheit vergessen: 1492 landet Kolumbus in Amerika. In der Folge bringen die Spanier ganze Schiffsladungen von Gold und Silber nach Europa. Der Geldsegen (++M, ca. mal 10) verbreitet sich über ganz Europa. Europas Wirtschaft wächst (+Q, ca. mal 1.66); die Kultur der Renaissance blüht auf. Aber auch das Preisniveau steigt an (++P) ? in den folgenden 150 Jahren auf das Sechsfache. In dieser Zeit formuliert der spanische Mönch Martin de Azpilcueta den Zusammenhang zwischen steigender Geldmenge und steigenden Preisen. Er entdeckt damit zweitausend Jahre nach den Chinesen die Quantitätsgleichung für den europäischen Kulturraum.
Inflation und Deflation
Ein extremes Beispiel für die Quantitätsgleichung folgt auf den Ersten Weltkrieg. Das Deutsche Reich ist geschlagen und braucht dringend Geld. Die Reichsbank lässt die Notenpresse laufen (++M). Die Wirtschaft läuft wie geschmiert (+Q), doch rasch wird alles teurer (+P). Es herrscht Inflation. Und Geld macht süchtig (+M, +P, +M, +P, +M). Bald kostet ein Brot am Abend schon doppelt so viel wie noch am Morgen. Die Flucht aus dem Geld setzt ein. Die Menschen kaufen, egal was. Geld wechselt die Hand wie die heisse Kartoffel. Seine Umlaufsgeschwindigkeit steigt (++V) und mit ihr explodieren die Preise (++P). Doch niemand will verkaufen. Ein Brot kostet eine Billion Mark, aber der Bäcker bietet nichts feil. Auf dem Höhepunkt der Hyperinflation sind sämtliche Druckereien des Reichs damit beschäftigt, Banknoten zu drucken. Dennoch hält die Vermehrung des Geldes (++M) mit dessen Entwertung (+++P) nicht mehr Schritt. Die Wirtschaftstätigkeit kommt zum Erliegen (--Q). Das Geld ist nur noch ein Spielzeug.
Das Pendel schlägt zurück: auf Inflation folgt Deflation: Nach dem Börsensturz von 1929 brechen Banken zusammen, und die Notenbanken halten das Geld zu knapp (--M). Preise und Löhne sinken (-P). Die Wirtschaft schrumpft (-Q), Millionen sind arbeitslos. Die Grosse Depression erreicht 1933 ihren Tiefpunkt. Erst die Abwertung der wichtigsten Währungen gegenüber dem Gold erlaubt den Notenbanken, den Geldmangel zu beseitigen (+M). Die Weltwirtschaft erholt sich.
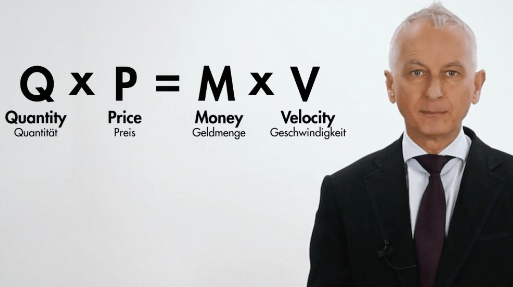
Die Gleichung gilt immer
Damit sind wir schon fast in der Gegenwart. 2007 sitzen die internationalen Grossbanken auf faulen Immobilienpapieren. Das Vertrauen schwindet. Die Banken leihen einander kein Geld mehr, die Umlaufsgeschwindigkeit sinkt (-V). Die Notenbanken befürchten einen Zusammenbruch der Wirtschaft. Sie pumpen riesige Geldbeträge (+++M) ins Bankensystem. Sie verhindern damit zwar das Schlimmste. Doch das Geld bleibt einstweilen untätig liegen; die Geldschöpfung verpufft in einem weiteren Rückgang der Umlaufsgeschwindigkeit (---V). Dennoch: Die Geldmenge ist ein schlafender Riese. Wenn das Geld in Schwung kommt, droht Inflation.
Die Quantitätsgleichung ist eine grosse Hilfe beim Beschreiben der monetären und wirtschaftlichen Entwicklung, von Inflation und Deflation. Sie sagt aber nichts über Ursachen und Wirkungen.
Die Notenbanken möchten die Wirtschaft gerne mit Hilfe der Geldmenge steuern (M). Sie wissen aber nicht, auf welche der anderen drei Grössen eine Veränderung der Geldmenge wirkt ? auf die reale Wirtschaftstätigkeit (Q), das Preisniveau (P) oder bloss auf die Umlaufsgeschwindigkeit des Geldes (V). Meist ist zudem die kurzfristige Wirkung eine andere als die langfristige.
Die Zusammenhänge zwischen den vier Grössen beruhen eben nicht auf Naturgesetzen, sondern auf den Entscheidungen von Menschen. Sie verlaufen deshalb nicht zu allen Zeiten gleich. Nur die Gleichung gilt immer.